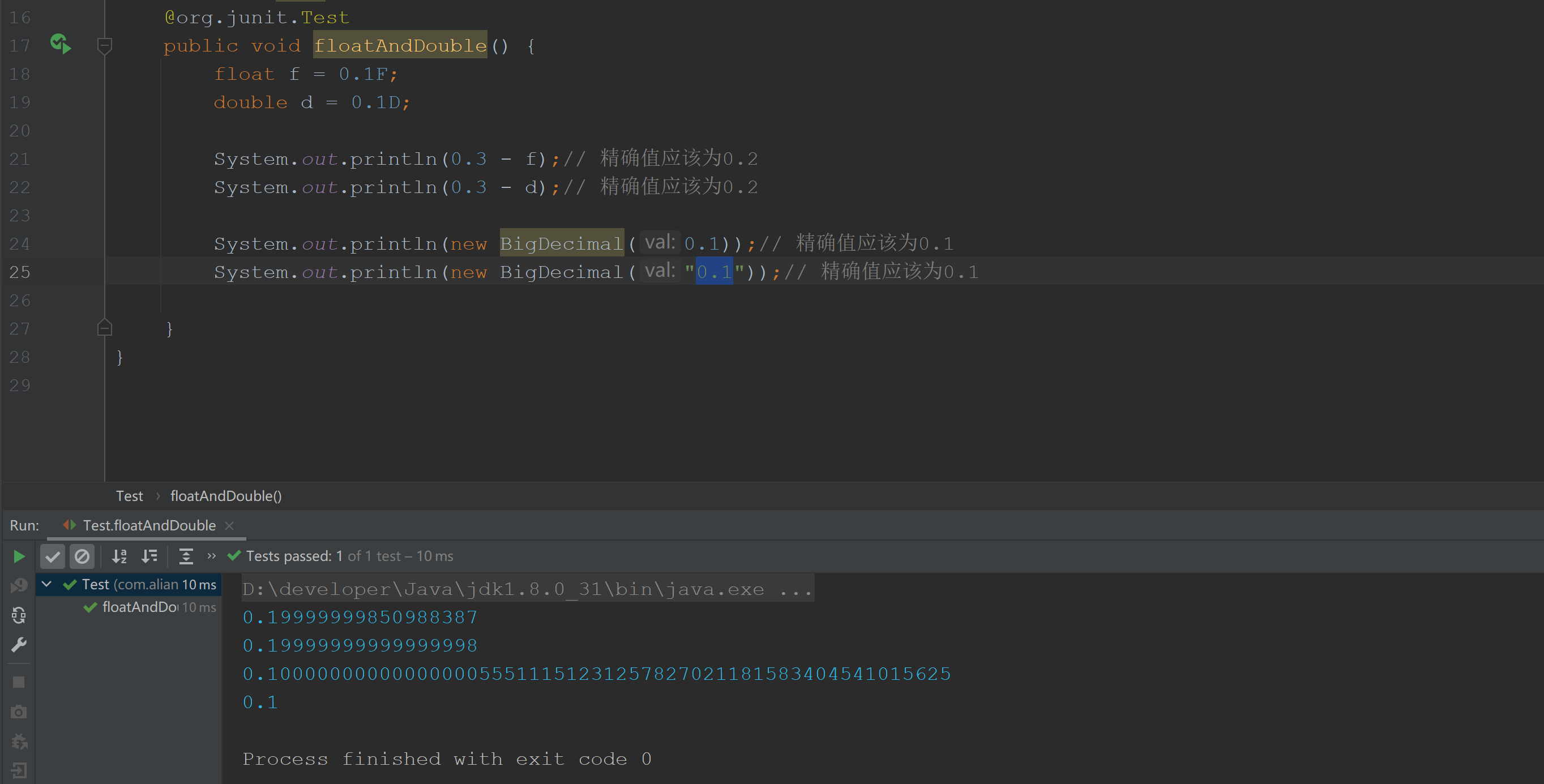
众所周知，在 Java 中，使用 float 和 double 分别用来表示单精度浮点数和双精度浮点数。
所谓精度不同，可以简单的理解为保留有效位数不同。采用保留有效位数的方式近似的表示小数，但是为什么需要以保留有效位数的方式来表示浮点数呢？难道就不能精确的表示吗？
答案是：float和double不能，但是BigDecimal 可以

float 和double为什么不精确

首先，计算机是只认识二进制的，即 0 和 1，这个大家一定都知道。
那么，所有数字，包括整数和小数，想要在计算机中存储和展示，都需要转成二进制。

十进制整数转成二进制很简单，通常采用 ”除 2 取余，逆序排列” 即可，如 10 的二进制为 1010,这个比较简单，在此不再细说。

但是，小数的二进制如何表示呢？
十进制小数转成二进制，一般采用 ”乘 2 取整，顺序排列”方法 ，如 0.625 转成二进制的表示为 0.101。

具体做法是：用2乘十进制小数，可以得到积，将积的整数部分取出，再用2乘余下的小数部分，又得到一个积，再将积的整数部分取出，如此进行，直到积中的整数部分为零，或者整数部分为1，此时0或1为二进制的最后一位。或者达到所要求的精度为止

但是，并不是所有小数都能转成二进制，如 0.1 就不能直接用二进制表示，他的二进制是 0.000110011001100… 一个无限循环小数
这里我们使用 乘 2 取整，顺序排列的方法来计算一下

0.1 * 2 = 0.2   -----> 取整数部分0
0.2 * 2 = 0.4   -----> 取整数部分0
0.4 * 2 = 0.8   -----> 取整数部分0
0.8 * 2 = 1.6   -----> 取整数部分1
0.6 * 2 = 1.2   -----> 取整数部分1
0.2 * 2 = 0.2    -----> 取整数部分0 （从此处又开始新的一轮循环）
所以 0.1 的二进制 为 0.0001100110011 无限循环小数

所以，计算机是没办法用二进制精确的表示 0.1 的。也就是说，在计算机中，很多小数没办法精确的使用二进制表示出来，这也就是为什么float 和double的值并不是精确的原因了，其只是在一定精度范围内表示一个浮点数

那么，这个问题总要解决吧。那么，人们想出了一种采用一定的精度，使用近似值表示一个小数的办法。这就是 IEEE 754（IEEE 二进制浮点数算术标准）规范的主要思想。

IEEE 754 规定了多种表示浮点数值的方式，其中最常用的就是 32 位单精度浮点数和 64 位双精度浮点数。

在 Java 中，使用 float 和 double 分别用来表示单精度浮点数和双精度浮点数。

至于为什么Bigdecimal可以精确的表示浮点数是因为Bigdecimal用无标度值和一个标度值来表示一个浮点数； 如 123.456 用bigdecimal来存储的时候，无标度值为123456(可以简单理解为将浮点数移除了小数点)，标度值为3（可以理解为是几位小数），这样，用二进制来存储 123456 和 3 是都可以完全精确表示出来的，计算机存储的浮点数自然也就是精确的了；

我们下次再细说使用 BigDecimal 来表示浮点数以及运算时的一些问题和注意事项

Q.E.D.